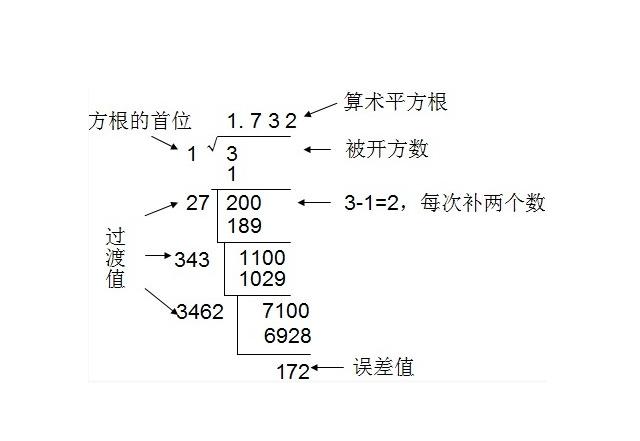
開平法のやり方と具体例 \sqrt{} の近似値を求めるという例を通じて開平法を解説します。 難しいのは手順4だけです。 まず \sqrt{} と右側に書く。 小数点を基準に2桁ずつ区切っていく。 二乗して「右側の最も左のブロック(この例だと 5 5 5 )」以下となるよう中学3年生 数学 平方根のいろいろな計算 問題プリント 無料ダウンロード・印刷 根号を含む複雑な式は、なるべく簡単な形に変形してから値を代入し、分配法則や乗法公式を使って√を含む式を計算する練習問題プリントです。平方根の長さを作図する2通りの方法 レベル ★ 基礎 平面図形 更新日時 任意の正の有理数 q q q に対して,長さ 1 1 1 の線分が与えられれば長さ
平方根是它本身的数有哪些 初三网
三平方根
三平方根-前ちゃんの中学校数学の部屋:パワーポイント補助教材3年 教材のダウンロード プレゼンテーション教材 3年 この教材を使用した授業方法は、 こちら をご参考にしてください。 ダウンロードに関する 注意事項 ダウンロードの前にお読みください「チャレンジテスト」に取り組んでみましょう 児童生徒の皆さんが家庭学習などで取り組むことができる 問題を作成しました。 ★ 北海道学力向上Webシステムについて ★ チャレンジテスト(第1回~) 著作権等の関係上、一部を除く問題を掲載しています。




平方根 數學符號 平方根 又叫二次方根 表示為 其中屬於非負數 百科知識中文網
6 平方根(3) ~根号をふくむ式の計算~ ホップ ステップ ジャンプ 7 2次方程式(1) ~平方根の考えを使った解き方・ 2次方程式の解の公式~ ホップ ステップ ジャンプ 8 2次方程式(2) ~因数分解による 平方根とルートの違い 平方根とルートは、似た状況で使われるため、全く同じ意味だと勘違いされやすいです。 まず、平方根の考え方を紹介しましょう。 2乗すると 9 9 になる数はなんでしょうか? その数を x x とすれば、 x2 = 9 x 2 = 9 という方程式を平方根 平方根(1) 問題一括 (8,085Kb) 解答一括 (9,324Kb) 平方根(2) 平方根の大小 有理数と無理数 平方根の乗法 平方根の除法 平方根の性質(1) 平方根の性質(2) 平方根の近似値 根号を含む計算 有理化 平方根の加法・減法(1) 平方根の加法・減法(2) 平方根の
Ⅰ 平方根の必要性 まずは、平方根という考え方が必要となった背景に迫ってみましょう。 平方根の起源は、紀元前6世紀頃の ピタゴラス(Pythacoras, BC569頃BC500頃)にまで遡ります。 ピタゴラスといえば、ご存知の通り、次の定理が有名です。イ 三平方の定理を具体的な場面で活用すること。 三平方の定理は直角三角形の3辺の長さの関係を表しており、数学においてとても重要な定 理である。中学校における三平方の定理の扱いは、証明について考えることよりも、利用に重 点が置かれている。三平方の定理とは ここは、数学のおさらいになります。三平方の定理がわかっている方は、読み飛ばしてください。 直角三角形があり、それぞれの3辺を x y z としたとき、3辺の長さは、 z 2 = x 2 y 2 が成り立ちます。これは、三平方の定理と呼ばれてい
この三平方の定理(ピタゴラスの定理)とは何かっていうと、 直角三角形の3つの辺の関係を表した公式 なんだ。 もうちょっと具体的にいうと、直角三角形には、 斜辺の2乗は、直角をはさむ辺を2乗して足したものと等しい っていう関係があるんだMath クラスで用意されている sqrt メソッドを使用すると、引数に指定した値の平方根を取得することができます。また cbrt メソッドを使用すると立方根を取得することができます。ここでは Java で数値の平方根または立方根を取得する方法について解説します。 中3 学習単元一覧 式の展開 因数分解 平方根 2次方程式 2乗に比例する関数 図形の相似 三平方の定理 円の性質 標本調査 式の展開式の展開の基礎乗法公式1乗法公式2



1到100平方根口诀表 西瓜视频搜索



平方根公式怎么算 如何计算平方根 学习岛
三平方の定理とは そもそも三平方の定理とは 直角三角形における3つの辺の長さの関係を表したものだ。 直角三角形の底辺の長さと高さをそれぞれ2乗し、 それらを合計した値の平方根は、斜辺の長さに等しい。 斜辺の長さだけに限らず、式を組み替えれば 三平方の定理の証明です。 先ほどの ベクトルの (x *xy* yz* z) の平方根の長さを返します magnitudeはベクトルの長さを返す。 (a b)^2 = c^2 4 (1/2ab) これを書き方だけ直すと c*c = a*a b*b なので雰囲気は似てきました。学習プリント画像をクリックすると問題が開きます。 解答が必要な場合は、下の一覧表の 解答(pdf) をクリックしてください。 一括(pdf) は 問題と解答 がセットでダウンロードできるようになっています。 練習問題とは、本研究委員会で作成した問題のことです。



初中数学平方根口诀表 初三网




平方根 三教学反思 学坛作文网
三平方の定理とは、直角三角形において 斜辺の長さの2乗は、他の辺の長さの2乗の和に等しくなる。 というものです。 文章だけでは、難しく見えますが 非常に単純な定理です。 このように 斜辺の2乗の数と 他の辺を2乗して足した数が等しくなるの二乗和の平方根と三平方の定理の関係 二乗和の平方根は、三平方の定理と関係します。下式をみてください。 c=a 2 b 2 d=√c 両辺を2乗すると、 d 2 =a 2 b 2 です。dを斜辺、a、bを底辺、高さと考えれば、三平方の定理(ピタゴラスの定理)となります。Myhypot では、 hypot と同じアンダーフロー動作とオーバーフロー動作についての検討はなされません。 myhypot が有用な値を返す上限を求めます。 この




三个数学符号的平方根 根png图片素材免费下载 图片编号 Png素材网




例題 求平方根 Youtube
「平方根」「根号」という言葉を しっかり理解することで解決します。 丁寧に整理するので、 以下を順番に読んでみてくださいね。 まずは基本の確認を! 「平方根」の求め方 について、 数学の基本をすでに説明したので、 まだ読んでいない中3生は、そもそも立方根とは??エクセルで立方根を計算する方法 それでは、まず立方根とはどのようなものであるか確認していきましょう。 ある数aを指定したときに、a×a×a=bという関係があるとき、aはbの立方根であるといえます。初等幾何学における ピタゴラスの定理 ( ピタゴラスのていり 、 ( 英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理 ( さんへいほうのていり ) 、 勾股弦の




3种方法来计算平方根的乘法



3开平方是多少3的平方根是多少 新绅网
三平方の定理の《平方》とは、同じ数字を自乗する(掛け合わせる)ことをいいました。 《平方根》は、その数字(数値)になるために掛け合わせられた、もとの数のことをいいます。 * たとえば、 1 の平方根 ( √ 1 ) は 1 で、 4 の平方根は 2 です。 まとめ:三平方の定理(ピタゴラスの定理)を使えば直角三角形の辺の長さは大体わかる! 三平方の定理で、直角三角形の辺の長さを求める問題はどうだった? 今日勉強した問題のパターンは4つだったな? 超基本タイプ;Hypot と根本的には同じ基本関数を実行する無名関数を作成します。 myhypot = @ (a,b)sqrt (abs (a)^2abs (b)^2);




最新平方根 立方根综合练习题定制版



平方根 禾教 初中数学互动课堂
2章 平方根 問題(pdf3480kb) 解答(pdf9227kb) 3章 2次方程式 問題(pdf413kb) 解答(pdf1099kb) 4章 関数y=ax 2 問題(pdf495kb) 解答(pdf502kb) 5章 相似な図形 問題(pdf4kb) 解答(pdf844kb) 6章 円 問題(pdf6kb) 解答(pdf696kb) 7章 三平方の定理



初一下平方根与算术平方根避坑题 附三道真题解析 哔哩哔哩 Bilibili




怎么进行平方根的加减法 最有妙招网




3种方法来计算平方根的乘法



2 平方根 北师大版八年级上册数学电子课本 数九网




平方根 數學符號 平方根 又叫二次方根 表示為 其中屬於非負數 百科知識中文網




Leetcode 69 Sqrt X X 的平方根 三九 感冒灵的博客 程序员信息网 程序员信息网



初中数学 平方根的易错题 哔哩哔哩 つロ干杯 Bilibili




平方根的练习题x 下载




平方根表 算术平方根表是什么 三人行教育网 Www 3rxing Org




人教版数学七年级下第六章6 1平方根 3 平方根 Ppt 8096 超级ppt




平方根 实数ppt 第3课时平方根 下载 牛二ppt




平方根公式初中數學平方根的計算公式 初三網 Tbtky




3数学的平方根n I 函数的零根png图片素材免费下载 图片编号 Png素材网




數三3 2平方根的運算 Youtube



平方根 实数ppt 第3课时平方根 第一ppt




计算方法 三 平方根法及其改进解线性方程组 M0 的博客 Csdn博客



已知一个数的平方根已知一个数的两个平方根分别是2x 1与3 X 那么这个数是



八年级数学上册第3章实数3 1平方根第1课时平方根和算术平方根教案湘教版




平方根 实数ppt 第2课时 下载 牛二ppt



Hdaxt Com




平方根 新人首单立减十元 21年11月 淘宝海外



Sx 7 019第六章6 1 3平方根 平方根导学案附教学反思 范文118




根据算术平方根定义来解题



立方根平方根



初中数学 求平方根问题不会做 总出错 一节课帮你搞定




6 1 1 平方根 综合练习 2 含答案 七七文库www 77wenku Com




根号口诀表 怎么巧记平方根 三人行教育网 Www 3rxing Org



七年级下数学课件 6 1 平方根 共25张ppt 人教新课标



平方根计算




6 1 3平方根3 第三课时 Ppt




3开平方等于多少 搜狗搜索




平方根表图 七年级数学平方表 平方根表是怎么看的 三人行教育网 Www 3rxing Org



初中数学求算术平方根 有人秒出答案 有人无从下手 原因在这儿




1 6数的开方与二次根式




3の平方根 Wikipedia




平方根 实数ppt 第2课时 下载 牛二ppt




平方根怎么算 如何快速算出平方根 环球信息网




加减平方根 建议 November 21



平方根 立方根 我的网站




三的平方根 搜狗搜索




算术平方根 平方根知识点 Doc 悦读文库




3种方法来不用计算器求平方根




3的算術平方根 维基百科 自由的百科全书




平方根 Wikiwand




翻转数学 第三章 平方和立方 平方根和立方根 Facebook




初一数学平方根考点详解 掌握题型 学会方法 楠木轩



3月26日 初一数学日常刷题 平方根 角度计算 哔哩哔哩 つロ干杯 Bilibili



平方根 數學名詞 公式 運算 描述 過程1 過程2 過程3 例子 牛頓疊代法 知 中文百科全書




怎么进行平方根的加减法 最有妙招网



平方根计算方法 数字计算方法 手动开方 尚书坊



初一数学 平方根 腾讯视频




平方根 新人首单立减十元 21年11月 淘宝海外




怎么简化平方根 最有妙招网



立方根 禾教 初中数学互动课堂




求解這三題我不會 Clearnote



平方根的概念 平方根和立方根的概念与性质 尚书坊



2 平方根 北师大版八年级上册数学电子课本 数九网




3的算術平方根 维基百科 自由的百科全书




怎么求平方根的值公式 怎么求数的平方根 三人行教育网 Www 3rxing Org




青岛版数学八上5 1 算术平方根 Wenkub



数学平方根 初二数学 上 知识点 平方根 尚书坊




平方根的练习题x 下载




求一个数的值和它的平方根有哪些区别 如 根号81 院勾问答




平方根的练习题x 下载



1



平方根是它本身的数有哪些 初三网




3种方法来计算平方根的乘法



平方根公式计算过程 初中数学平方根的计算公式怎么算更简洁 学习岛




3的算術平方根 维基百科 自由的百科全书



二次平方根公式 二次平方根的运算依据什么 学习岛




三的平方根 搜狗搜索



19中考数学复习练习2平方根 一 无答案 淘文库




如何手算平方根 包含图片




数学 中学3年7 平方根3 Youtube




根号4的算术平方根是多少48的平方根等于多少48的平方根和算术平方根为多少



负根号3有意义吗为什么 初三网




部编版七年级数学下册平方根用计算器求算数平方根及其大小比较课件ppt模板下载 熊猫办公




平方根练习题 Doc 文档分享网



平方根 实数ppt 第3课时平方根 第一ppt




03立方根实数初中数学初二 Youtube




平方根练习题 Doc 文档分享网




3的平方根 怎样计算一个数的平方根 52fmz购物网




中3数学 8 3 平方根 Youtube



七年级数学下册 平方根知识和例题 根号81的平方根是 3还是 9




3的平方根 怎样计算一个数的平方根 52fmz购物网



3开平方是多少3的平方根是多少 新绅网



上海市数学中考知识点总结 新 伴学郎辅导




计算方法 三 平方根法及其改进解线性方程组 M0 的博客 程序员宅基地 平方根法解线性方程组 程序员宅基地




三平方根 Pksubra




加减平方根 建议 November 21



精选二四六天天好彩头 蓝月亮二四六精选大全 二四六好图片玄机图小说
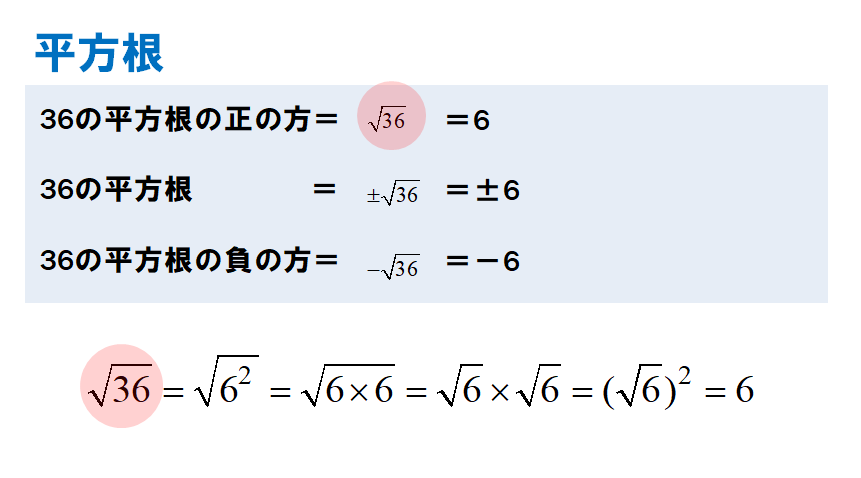



中3数学 平方根の性質の定期テスト対策問題 Examee




16算他的算术平方根16的平方根和算数平方根是什么



0 件のコメント:
コメントを投稿